Add Inference: Yet another 7 weeks
The Course
Content will be updated from time to time, so please refresh frequently.1
Syllabus
Description
In the System Dynamics Inference course we apply Bayesian data analytics to calibrate, fit, simulate, and infer conclusions consistent with the causal model of the decisions we are studying. The causal model will be built in VensimPLE, read into R, where we can mash the model with data and use Stan to make probabilistic inferences. During the first 5 of 7 weeks we will build basic system dynamics causal models of various business decision, estimate probability models of decisions based on the causal models, and infer probabilistic results using Machine Learning and information criteria.
- For these courses we will cross three computing platforms. VensimPLE will help us build and simulate generative causal models, visualize results, and develop scenarios for decision makers. The R programming language (with R Studio - Posit), the tidyverse of data, optimization, numerical integration, and visualization packages will provide a platform for analysis, inference, and visualization of results. The Stan (for Stanislaus Ulam) probabilistic programming library with its ability to estimate systems of differential equations (the underlying mathematics of system dynamics) using Hamiltonian Monte Carlo simulation will allow us to estimate the uncertainty within the causal models we have built.
Resources
Readings
The main resources for the course are these books and articles (more of each in the following weeks):
Jim Duggan, System Dyanamics in R, 2016. rentable and for purchase online edition is accessible here.
William G. Foote. 2022. Stats Two: Bayesian Data Analysis using R, Stan, Rethinking, and the Tidyverse. Access here. This book compiles much of the material needed for the course from other sources and on its own. It is inspired by E.T. Jaynes Theory of Probability: The Logic of Science and a pre-print copy is in this directory. and owes most of its impetus, and not a few of the models, from the next resource by Richard McElreath.
Contemporary statistical inference for infectious disease models using Stan. Epidemics 29 (2019). Anastasia Chatzilenaa et her colleagues have compiled a well-worked explanation of the basic Bayesian model structures for inferring conclusions from system dynamics models. Abstract: This paper is concerned with the application of recent statistical advances to inference of infectious disease dynamics. We describe the fitting of a class of epidemic models using Hamiltonian Monte Carlo and variational inference as implemented in the freely available Stan software. We apply the two methods to real data from outbreaks as well as routinely collected observations. Our results suggest that both inference methods are computationally feasible in this context, and show a trade-off between statistical efficiency versus computational speed. The latter appears particularly relevant for real-time applications.
System Dynamics Review - 2021 - Andrade and Duggan - A Bayesian approach to calibrate system dynamics models using Hamiltonian Monte Carlo. This, along with Jair Andrade’s calibration tutorial will provide much of the core of our 7 week journey through this topic.
Gelman and Shalizi’s Bayesian Hypothetico-Deductive Methodology (2013). Do we agree with this fairly scathing approach? There are excellent examples of the inferential process implied by Bayesian analytics of which we well need be aware.
Tom Fiddaman’s Vensim Calibration notes. We will be using some of the workflow here. However, most of that tasking will be inside of R with Stan.
R for Graduate Students. Simply, and very cohesively, arranged and developed introduction to R using the tidyverse.
Basic beginning R tutorial (Rmarkdown) Rmarkdown and rendered pdf can get us started.
Additional resources
Richard McElreath. 2020. Statistical Rethinking: A Bayesian Course with examples in R and Stan details through this site We will be working through elements of the first 5 chapters, but will move quickly to the next to the last chapter on Lynx and Hare competition.
Trevor Hastie, Robert Tibshirani, and Jerome Friedman. 2009. Elements of Statistical Learning: Data Mining, Inference, and Prediction, Second Edition, Springer Science & Business Media, 2009. The authors have a tutorial site with a downloadable edition of this book, R scripts and other materials accessible here. These authors are at the tip of the machine learning spear in the frequentist tradition.
Yanchang Zhao, Data Mining with R. 2020, online with books, slides, datasets, R scripts, numerous examples here, all from the frequentist tradition of model formulation, inference and interpretation.
Weekly live sessions will expand on key aspects of chapters from Duggan, Foote and McElreath, and others as needed, and prepare us for weekly assignments. Vensim mdl models, R scripts, Stan code, along with RMarkdown source files, and data sets accompany each week.
Access
VensimPLE
With your Manhattan University sign-on credentials use Manhattan University remote desktop (DLS 210, 309 or 314 to access VensimPLE.
Download (for free) VensiMPLE. Choose your Windows or Mac OSX platform, your email, and you will receive instructions to follow.
R and Stan
Access R in several possible ways:
With your Manhattan University sign-on credentials use Manhattan University remote desktop (DLS 210, 309 or 314 to use R Studio, the integrated development environment (IDE) we will use.
Use the RStudio cloud platform. This option does not support the Stan library and the cmdstanr package, yet. It does support the slimmed down rethinking package, which will suffice for our first 3 weeks.
Click here to download a document with details about installing R and preparing your computer for R analytics and see as well as Long and Teetor (2019, chapter 1)
Note: Chrome users may need to right-click and select Save Link As to download files.
Data
Most of the data for the course comes from R packages such as rethinking@slim, a non-Stan version of rethinking both by Richard McElreath.
Set up a working directory on your computer by creating an R project in RStudio. Typically this is located in the user’s documents directory. With this working directory go to RStudio and create a new project to you will save your files.
Within the working directory, you can set up a data directory called
data. This is a sub-directory of your working directory.
When you set up an R Project in a directory, forever more that directory will be your working directory for a particular project, at least for the work being done in that directory. Choose other directories to set up other projects.
Statistics tutorials
The practice of business analytics benefits greatly from advances in statistics and operations research. Here is a statistics primer that we can use to refresh our understanding and use of basic concepts and models often deployed in business analytics. You can access the Statistical Thinking site here
Requirements
The course is officially online. However optional live sessions each week (they will be video’d!) will help keep all of us awake to one another’s needs throughout the course.
There are six (6) assignments to be submitted through a course workbook (a Google form). In addition there is a participation grade.
Assignments 1 through 5 are each worth 13% of the final grade, that is, for a total of 65% of the final grade. These will be completed during weeks 1 through 5 of the course. They will typically include an upload of a model and a short interpretation of results.
Assignment 6 is worth 25% of the final grade and will be completed during weeks 6 and 7 of the course. This last assignment is designed to pull course concepts together into a comprehensive system dynamics model replete with interpretation and ready for policy analysis.
Participation is worth 10% of the final grade. This grade will be primarily evidenced through posted comments on the course blog site regarding modeling vignettes and issues.
We will work in teams and submit individual assignments and posts. Individual grades are A-F (integer ranges): A (>95), A- (90-94), B+ (85-89), B (80-84), C+ (75-79), C (70-74), D (65-69), F (<65).
Weekly course schedule
Here is a summary of the weekly topics.
| Week | Topic | Notes |
|---|---|---|
| Week 1 | Building a generative model of decision maker interaction: collaboration and competition | Simulating a decision anthropology of gift with Lotka, Volterra, and Schindler |
| Week 2 | Endogenizing external factors and limiting growth and innovation | Constraints on decision maker innovation in markets with Meadows, Guardini, and Hirschfeld |
| Week 3 | Counting with Bayes to infer (learn) | Updating knowledge to infer decision consistencies with McElreath, Ockham, and Jaynes |
| Week 4 | Acting on Bayes to build decision alternatives consistent with data | The classic two state - two decision model with Zellner, Laplace and Lagrange |
| Week 5 | Inferring the impact, uncertainty and predictability of decision tradeoffs | An inference machine for language and diversity with Watanabe, Nettle and Searle |
| Week 6 | Expectations formation, learning, priooritization, and managerial decisions | Decision inference in a behavioral model with Sterman, Turing, and Aquinas |
| Week 7 | Compendium: final case preparation and presentation | A trolley ride with (Philipa) Foot |
Other matters
Academic integrity
The Manhattan University Academic Integrity Policy holds students accountable for the integrity of the work they submit. Students should be familiar with the Policy and know that it is their responsibility to learn about instructor and general academic expectations with regard to proper collection, usage, and citation of sources in written work. The policy also governs the integrity of work submitted in exams and assignments as well as the veracity of signatures on attendance sheets and other verifications of participation in class activities. For more information and the complete policy, see the Manhattan University Catalog.
Students with disabilities
If you need academic accommodations due to a disability, then you should immediately register with the Director of the Specialized Resource Center (SRC). The SRC at Manhattan University authorizes special accommodations for students with disabilities. If you have a documented disability and you wish to discuss academic accommodations, please contact me within the first week of class.
Week 1
Getting Started: a basic predator-prey model
Together we will
Review the course, formation of teams, logistics, requirements, ground rules.
We will also download VensimPLE, R, and R Studio (Posit) and work with simple models to get a feel for the modeling platforms.
Most importantly we will deploy a 6-step approach to analyze the business side of a question we will pose. A model will emerge on a one-page piece of paper.
After we design, and begin to specify components of the model, then, and only then, will we open first Vensim, then R Studio, and translate the paper model into a computable model.
This week we will introduce ourselves to the primordial interaction model, originally called the preditor-prey model of biological population dynamics, discovered independently by Lotka and Volterra. Definitely check out the excellent Scholarpedia article by Frank Hoppensteadt, “Predator-Prey”, Courant Institute of Mathematical Sciences, NYU, New York, NY of the Courant Institute of Mathematical Sciences, NYU, New York, NY and James K. Galbraith’s 2006 Mother Jones article, “The Predator State”, for an application to our polity.
Along the way we will introduce ourselves to one another on THE WALL and review system archetypes from time to time, for example, this article on system dynamics by John Sterman from MIT, and this address by Donnella Meadows on systems thinking for sustainability.
We will also explore ways to communicate our results, for example this rendering of Barbard Minto’s Pyramid Principle.
Dates to Remember
Tuesday 2024-03-05 to Monday 2024-03-11 online
Live session Saturday 2024-03-9 from 10:00 to 12:00 (Eastern Time; UTC -5) on Bill Foote’s Zoom link.
Zoom: https://us06web.zoom.us/j/4915046043?pwd=lRcmR6raK50vawabuxzl3fWECDGZYO.1
Enjoy the View
All videos are on the System Dynamics: Bayesian Inference and Calibration playlist on my Youtube channel. Here is the link to the playlist.
Video 1: Course Overview This 45+ minute video ranges across the syllabus, key concepts, and an example of the work of system dynamics in the context of Bayesian inference.
Video 2: Course Foundations: The primordial preditor-prey model. In this inaugural episode of the Bayesian inference of a system dynamics model, we dive into the deep end of the pool with a Lotka-Volterra predator-prey model. Well, let’s get rid of the predation piece! Really, this is the basic model of interaction among entities. This will be our working model for the next few weeks. It has all of the features of a simple enough representation of complex interactions among various entities. Here WolfCo uses pricing to influence MooseCo customers to switch to WolfCo. The model can just as easily be a new technology dependent on a component technology, or an analytics capability depending on a sole-sourced component capability, or again, a conflict minerals NGO exploited by commercial interests. Supply chains, innovation, governance, profit, not-for-profit, all can be represented by variations of this primordial model. Here we walk through the definition of system dynamics, stocks, flows and loops, with Aristotle’s four causes. All of this is linked to an empirically challenged process of Bayesian Inference. All on pencil and paper! Chapter 1 of Duggan will be our guide. Notes for this episode are available here.
Video 3: MooseCo and WolfCo get Vensim-ed. Whatever we built with a Ticonderoga No. 2 pencil on engineering paper we translate into Vensim. In this episode we build a Vensim model of MooseCo and WolfCo customer base interaction. In the process we use a- prefixed auxiliary, s- prefixed stock, and f- prefixed flow variables and entities, in our own internal language. This follows the practice by Jim Duggan which will facilitate our move through the XMILE file conventions to R. We finish with two custom graphs and enjoy the views.
Video 4: Paper, Pencil, Moose, Wolf, R, HTML In this episode we take our paper and pencil interaction model (Lotka-Volterra system) to R, through RStudio, with a simulation function, and the tidyverse. We use a version of Richard McElreath’s Rethinking Statistics simulation for hares and lynx. We build an interactive plotly graph with ggplot2. Even better than that we knit the whole thing together using rmarkdown into an HTML file most anyone with a browser can read AND the interactive ggplot2-plotly graph is still interactive. Yikes. What’s next? Graph labels, better parameter packing, more useful written commentary, another layer in the model, using deSolve ODE solver. So much more to do and learn. Ready for a logistic growth version of this model? This is something to look forward to in Week 2. As always enjoy the view.
Download moose-wolf.mdl to a working directory locally then open the file in VensimPLE. While in VensimPLE go to Simulation > Start SyntheSim to see sliders appear. Now we can tickle those ivories a bit and watch the graphs dance around.
Download wolf-meets-moose.Rmd and knitted wolf-meets-moose.html to follow along the discussion of the two entity interaction model as R might have it. This model will be refreshed a few times as we meander through two ways to simulate the model.
Reading is Fun
We will stick to some basics this week.
Duggan, Chapters 1 and 2. We begin by building a simple system dynamics model. Using a simple model we will read the model into R, and solve, simulate, and visualize the model.
Foote, Chapter 1. We get acquainted with the Reverend Bayes. We can also take a look at chapter 3 to get some practice with R.
Let’s Do Somthing Interesting and Evaluate Our Progress
For those registered in a current Manhattan University MBA course, access the weekly grade assignment activity on the course Learning Management System (Moodle) and post your response there for credit. For those who are self-studying, you may access the Workbook.
Detail the 6 steps we took to build the customer base interaction model. Instead of a customer base, choose another complex of interactions, just two, such as supply and demand. Paper and pencil the model replicating the 6-Step design approach notes on a single page.
Download the moose-wolf Vensim model. Modify the variable names to fit your example in 1. Run the model successfully. Interpret the results.
Download the moose-wolf Rmd file and modify the variable names to fit your example in 1. Run the model successfully. Compare the results with your Vensim model. Can you formulate your model in a spreadsheet based on a download of Vensim model equations?
Week 2
Getting Started: endogenizing our limits to predation
Together we
Review what we have accomplished so far.
We expand our model to include a way to answer questions about capacity and limits to growth.
We will learn to read a Vensim mdl model into R using the R
readsdrpackage. As if that was not enough, we will solve the model using thedeSolvepackage.One more wrinkle in the highly textured manifold of this course: we will begin to understand the very basics of Bayesian data analytics using a simple grid approximation approach to mashing together data and hypotheses about the data.
We will continue to explore ways to communicate our results, for example this rendering of Barbara Minto’s Pyramid Principle. In line with this segment we will experiment with the
flexdashboardpackage for communicating results to clients.
Dates to Remember
Tuesday 2025-03-17 to Monday 2025-03-23 online
Live session Saturday 2025-03-22 from 10:00 to 12:00 (Eastern Time; UTC -5) on Bill Foote’s Zoom link.
Zoom: https://us06web.zoom.us/j/4915046043?pwd=lRcmR6raK50vawabuxzl3fWECDGZYO.1
Enjoy the View
All videos are on the System Dynamics: Bayesian Inference and Calibration playlist on my Youtube channel. Here is the link to the playlist.
Video 1: “From the Inner Mind to the Outer Limits” to growth that is: adding endogenous capacity to the model. Welcome to Week 2 with this first episode. We review what we think may have happened during Week 1’s excursions into system modeling of a predator-prey (Lotka-Volterra) model of customer predation. We built the model by hand on paper with pencil, then in Vensim with stocks and flows and two graphs, then in R with a simulation function and ggplot2 interactive plotly graphics. This week more of the same with two major wrinkles. Wrinkle 1: we further curtail growth by using capacity to build in a discount factor; Wrinkle 2: we endogenize capacity with a non-renewable stock of customers. Again, more Vensim and R will follow. But this week we wander into a Bayesian hypothetical-deduction frame of mind to infer plausible parameter values for a system. Enjoy as always.
Video 2: Endogenized Capacity Limits to Growth a la Vensim. In this second episode of Week 2 we dampen the predator and the prey’s customer acquisition rates using a customer availability discount based on market capacity. But we did not stop there as we fumbled forward to build an overall available customer base with a MooseCo and WolfCo rule to allocate time dependent market capacities for the two enterprises. ur next step will be to try to explain the new dynamics to ourselves and others; playing around with the Vensim slide bars. Our next episode will read this model into R and after that we will build a probabilistic generative model. Phew! and of course enjoy! The (nearly) completed model is here: wolf-moose-limits.mdl as you follow through the build process.
In these Week 2 notes we work through a different allocation rule than the video, \(\phi(t)\), based on the ratio of MooseCo to total market (MooseCo plus WolfCo) customers.
\[ \phi(t) = \frac{M(t)}{M(t) + W(t)} \] To determine the MooseCo time \(t\) capacity \(K_M(t)\) we incorporate the customer stock at simulation time \(t\), \(C(t)\). Similarly, we calculate the WolfCo time \(t\) capacity \(K_W(t)\).
\[ K_M(t) = \phi(t) C(t) \] \[ K_W(t) = (1-\phi(t)) C(t) \]
We can well ask: How many exogenous auxiliary variables remain?
Video 3: Rendering our simulation in R two times. In this episode, well, it is a lot!
Upgraded the Vensim model for capacity limits to growth;
Further upgraded the model to endogenize the capacities by introducing a market from which MooseCo and WolfCo can draw customers;
We then solved the model directly in R, repurposing our previous work and producing an interactive visualization using ggplot2 and plotly; we happened to use an integration method called euler;
We learned how to read the Vensim model into R using the readsdr package and peer into its contents;
From there we managed to solve the model using the deSolve package and the
rk4, 4th order Runge-Kutta approximate integration technique, which we also investigated a little bit;Last and the penultimate goal of all of these exercises we generated data by rerunning the model each time taking a sample of prior unobserved data from the acquisition rates;
Let’s not forget the 2 dimension scatter plot of generated data using the
geom_density_2d()andgeom_quantile()features from ggplot2.
We can download wolf-meets-moose-limits-to-predation.Rmd and the HTML, and interactive, knitted version wolf-meets-moose-limits-to-predation.html to follow along the discussion of the two entity interaction model as R might have it and how we generate synthetic data to examine the role of uncertainty on model variables.
Reading is Fun
Duggan, Chapter 3. We begin by building a simple system dynamics model. Using a simple model we will read the model into R, and solve, simulate, and visualize the model.
Try to run this model from Duggan, Chapter 3, in R. Use the comment # operator to document what you think is going on when we call the R codes.
library(deSolve) # solves system of differential equations
library(ggplot2)
library(scales)
START <- 2015; FINISH <- 2030; STEP <- 0.25
simtime <- seq(START, FINISH, by=STEP)
stocks <- c(sCustomers = 10000) #s for stock
auxs <- c(aDeclineFraction = 0.03) #f for flow
model <- function(time, stocks, auxs){
with(as.list(c(stocks, auxs)),{
if(time < 2020)
gf <- 0.07
else if(time < 2025)
gf <- 0.03
else
gf <- 0.02
fRecruits <- sCustomers * gf
fLosses <- sCustomers * 0.03 # hard-coded!
dC_dt <- fRecruits - fLosses
return (list(c(dC_dt),
Recruits = fRecruits,
Losses = fLosses,
GF = gf,
DF = 0.03))
})
}
o <- data.frame(ode(y =stocks,
times = simtime,
func = model,
parms = auxs,
method = "euler")
)
p1<-ggplot()+
geom_line(data=o,aes(time,
o$sCustomers,
color="Customers"))+
scale_y_continuous(labels = comma)+
ylab("Stock")+
xlab("Year") +
labs(color="")+
theme(legend.position="none")
p1## Warning: Use of `o$sCustomers` is discouraged.
## ℹ Use `sCustomers` instead.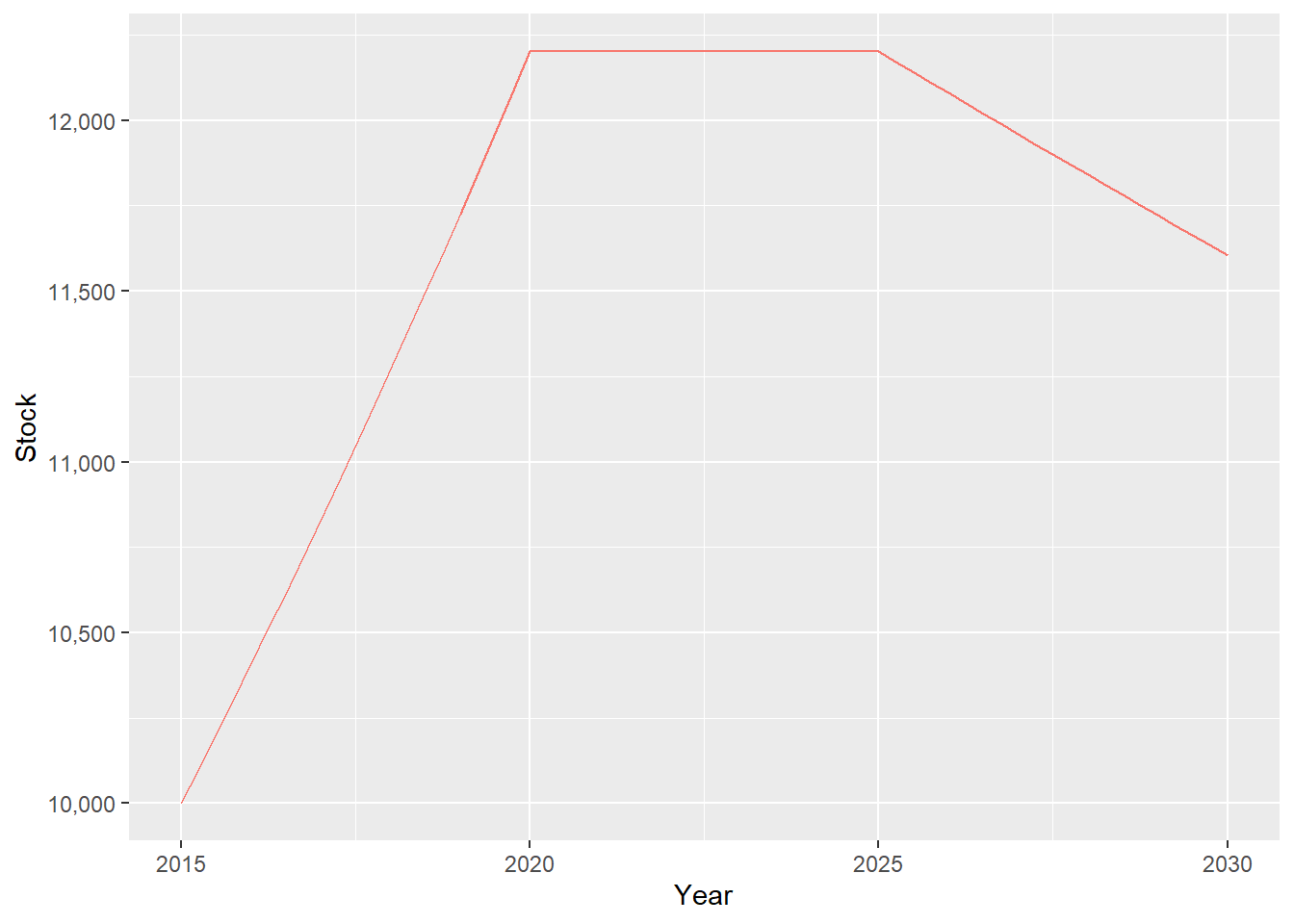
p2<-ggplot()+
geom_line(data=o,aes(time,
o$Losses,
color="Losses"))+
geom_line(data=o,aes(time,
o$Recruits,
color="Recruits"))+
scale_y_continuous(labels = comma)+
ylab("Flows")+
xlab("Year") +
labs(color="")+
theme(legend.position="none")
p2## Warning: Use of `o$Losses` is discouraged.
## ℹ Use `Losses` instead.## Warning: Use of `o$Recruits` is discouraged.
## ℹ Use `Recruits` instead.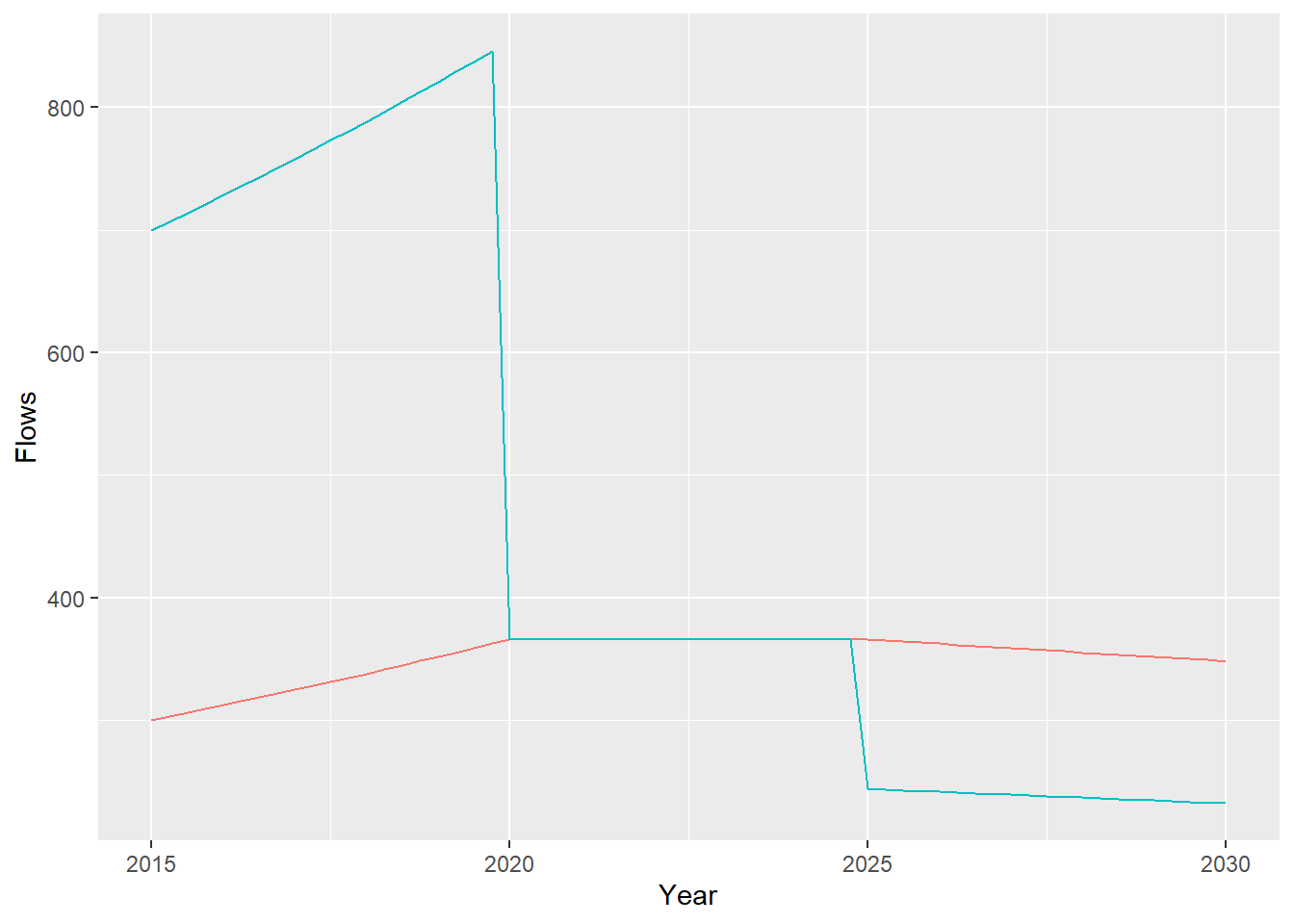
Let’s Do Somthing Interesting and Evaluate our Progress
For those registered in a current Manhattan University MBA course, access the weekly grade assignment activity on the course Learning Management System (Moodle) and post your response there for credit. For those who are self-studying, you may access the Week 2 Workbook here.
For the Public Benefit Corporation example from Week 1,
Modify the Vensim model for Week 2 to comply with your example. Describe the modifications.
Read the Vensim model into R and generate data from the model adding sampling from
aMooseSwitchingRateandaWolfSwitchingRate. Visualize the generated results.Interpret the generated joint distribution of the interaction of the WolfCo and MooseCo customer bases.
Week 3
Getting Started: infer to learn, then decide
This week we walk into the probabilistic expression of inference.
We start with a discussion of how to infer, statistically that is, which basically is a creative way to count.
We pause for a Bayesian interlude to discover a function relationship between observed data and unobserved hypotheses using rational integers and a simple algebraic rule, and certainly no calculus.
We move on to use our our counting method in a decision format, with a coding spree in R to support our calculations using a Gaussian distribution observational model of the data.
From there we (finally) use our MooseCo-WolfCo generated data to estimate the relationship between the two customer bases, something we began with the 2D density overlaid onto a scatter plot. We will introduce ourselves to a High Probability Credibility Interval (HPCI) to infer something interesting about the relationship.
Dates to Remember
Monday 2025-03-10 to Sunday 2025-03-16 online
Live session Saturday 2025-03-15 from 10:00 to 12:00 (Eastern Time; UTC -5) on Bill Foote’s Zoom link.
Zoom: https://us06web.zoom.us/j/4915046043?pwd=lRcmR6raK50vawabuxzl3fWECDGZYO.1
Enjoy the View
All videos are on the System Dynamics: Bayesian Inference and Calibration playlist on my Youtube channel. Here is the link to the playlist.
Video 1: Basic Bayes – Counting the Ways. This week’s task is to take our model to data for the purpose of learning something about the data. We have worked hard to build a causal model which we then used to generate synthetic data for two customer bases. In this episode we introduce ourselves to an hypothetical-deductive principled approach to probabilistic inference. It is Bayesian in nature, but in the end it simply indicates the plausibility of a range of mutually exclusive - completely exhaustive (MECE) hypotheses (our causal model for instance) consistent with sampled data we collected. We will use this model with various observed (samples) and unobserved (hypotheses) data to help inform us of tradeoffs in decisions.
Video 2: A Bayesian Interlude. In this episode we give plausible expression to a fundamental relationship we will discover between observed data and unobserved hypotheses. The relationship allows us to invert conditional probabilities. The Reverend Thomas Bayes discovered this rule based on a suggestion by Abraham deMoivre. It was all but abandoned to a frequentist approach led by Ronald Armyle Fisher. The Bayesian approach is (probably!) better named a probabilistic approach to inference. In most textbooks there is a puny chapter devoted to Bayesian calculations and usage. In this course, there is only a short reference to the relatively less principled frequentist approach learned as the mainstay in nearly all basic statistics course. There, you just had the short, and nearly the only reference, to a frequentist approach. Absolutely no calculus is required here, just the ability to count up to 17, work with rational integers, all with the algebraic knowledge that any integer divided by itself is the integer 1 and that any integer or algebraic expression for that matter times 1 is just itself.
Video 3: Acting on Bayes. We situate our need for a probabilistic approach which marries data to hypotheses in a principled, actually an algebraicly intelligible, way. Conditional probabilities abound here, ensconced in a 2-decision x 2-state decision frame where states are just hypotheses in decision clothing. We derive rules by which a decision could be supported, but here we are really interested in estimating a probability that a state occurs given the data available. We do so by hand and by R.
Reading is Fun
Read Duggan, Chapter 4: Higher Order Models. Get enough out of the chapter to begin to tackle the analysis of the cohort model in Exercise 1 for programmer career development at the end of the chapter.
Read Foote: Counting the Ways to get us in the mood for Bayes. Read and follow along by running the R code in Acting on Bayes, p. 1-9 (for now) to generate a principled, algebraicly intelligible approach to estimating probabilities and informing decision trade-offs.
The Week 3 Inference notes I used for the videos are available here.
If we feel the need to read ahead then by all means we should check out Hypothesis Testing to provide grist for our inferential mill and Causal Cats at least the generative modeling piece. WAIC might wait a bit. We’ll see!
Let’s Do Somthing Interesting and Evaluate Our Progress
For those registered in a current Manhattan University MBA course, access the weekly grade assignment activity on the course Learning Management System (Moodle) and post your response there for credit. For those who are self-studying, you may access the Week 2 Workbook here.
- This template is based on p. 6 of the Week 3 inference notes. Your job is to fill out this template with data and calculations. Use whatever story you would like to interpret the binary choices in the data coded as 0’s and 1’s.
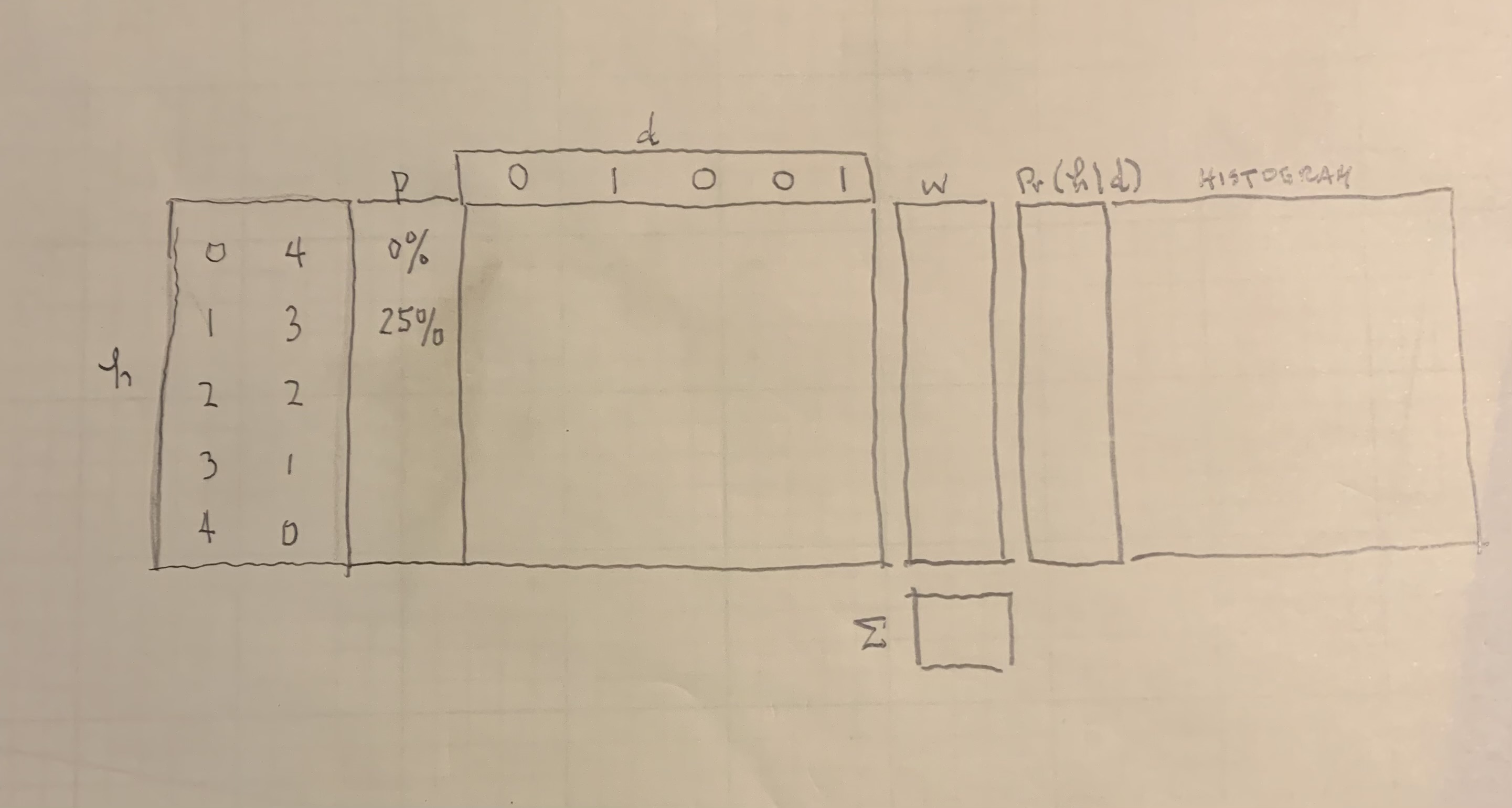
Template for Question 1.
- Here is a template based on p. 9 in the Week 3 Inference notes on the website. Fill in the numbers and show your calculations. Interpret your findings using whatever story you are using for the states (S) and decisions (D). Be sure to upload an image of your work below.
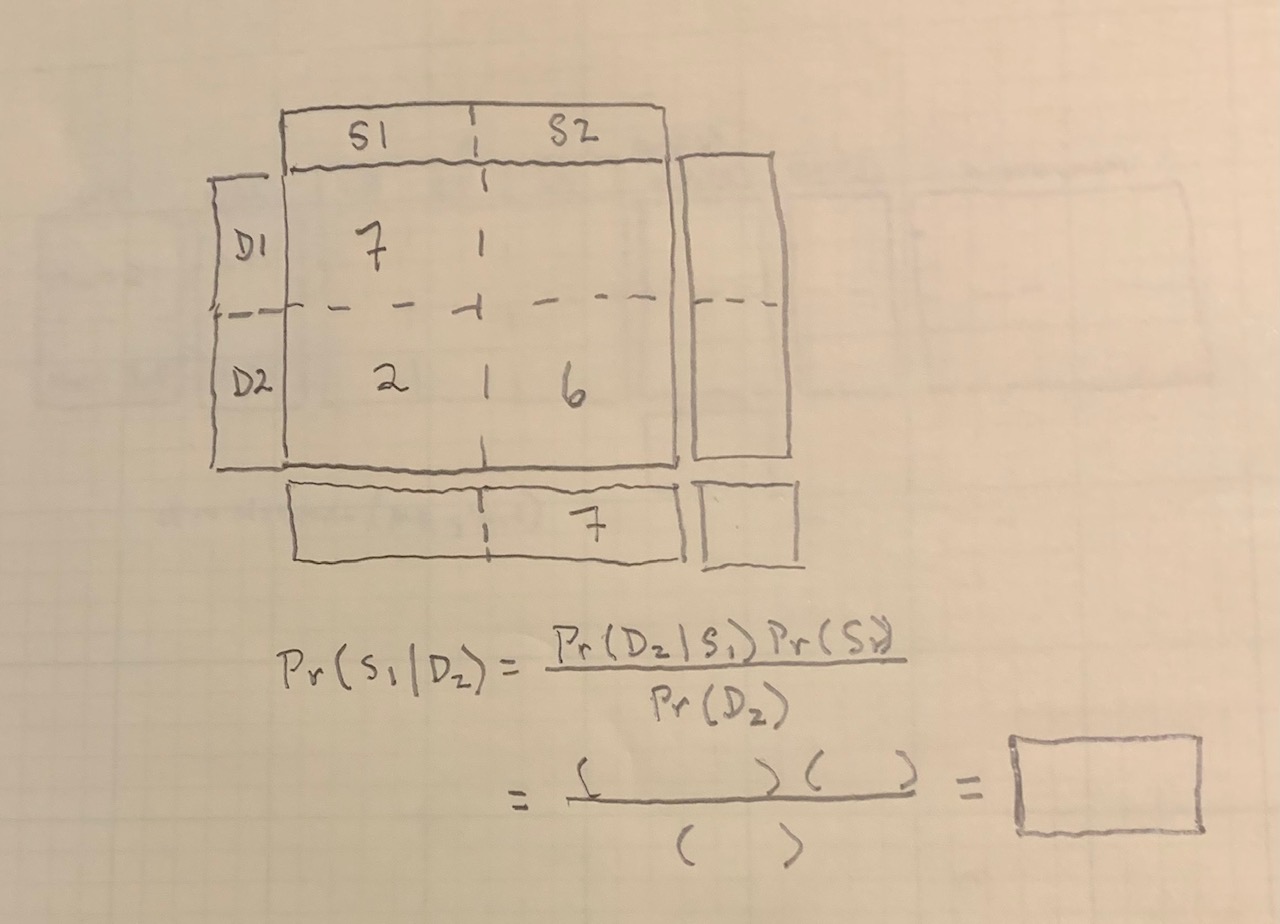
Template for Question 2.
- This R code is from pages 7-8 of the Acting on Bayes reading.
library( tidyverse )
#library( rethinking )
library( Rfast ) # for column products
set.seed(42) # this will produce the same
# pseudo-random numbers each time we run this
# code
y <- c(3.87, 1.94, 2.36)
d <- tibble(
y = y
)
# make grid of hypothetical mu
mu <- c(1.0, 3.0)
sigma <- 1
pr_h <- rep( 1, length(mu) ) / length(mu)
#equally likely
# we sample to get an idea
pr_d_h <- sapply(mu, function(mu) dnorm(y,mu,sigma))
colprods(pr_d_h)
likelihood <- colprods(pr_d_h) * pr_h
posterior <- likelihood / sum( likelihood )
posterior
which.max( posterior )
mu[ which.max(posterior)]Modify the code for this data:
y <- c( 3.2, 4.6, 1.7, 2.1 ) mu <- c( 1, 3, 5 )
Run the code. Comment every line of the code to document the calculations. If you are on a spreadsheet platform, replicate the calculations on a worksheet. In any case, most importantly, interpret the results.
Week 4
Getting Started: validate twice, decide once, repeat
Yikes! We get to WAIC up!
We count with the Marquis de Laplace this week. We will develop a quadratic approximation to replace our brute force grid approximation.
Then we will learn to generate samples of parameters and predictions, high density probability intervals, and very professional looking graphs to visualize our work and explain it to our relatives.
If that was not enough, we will wander into a discussion about the Widely Available Information Criterion, use leave-one-out cross validation (so Machine-Learning we will be), and with point-wise accuracy pin-point highly influential observations. This will, we hope, replace F-tests and \(R^2\) for good!
Ah yes, we will run many regressions.
We may even attempt to install the cmdstanr R package interface to the probabilistic programming library Stan. If not, we have not a few work arounds!
Dates to Remember
Monday 2025-03-31 to Sunday 2025-04-06 online
Live session Saturday 2025-04-05 from 10:00 to 12:00 (Eastern Time; UTC -5) on Bill Foote’s Zoom link.
Zoom: https://us06web.zoom.us/j/4915046043?pwd=lRcmR6raK50vawabuxzl3fWECDGZYO.1
Enjoy the View
All videos are on the System Dynamics: Bayesian Inference and Calibration playlist on my Youtube channel. Here is the link to the playlist.
Video 1: Counting on Laplace. In this lengthy episode we kick off week 4 with a grid approximation of a binomial model of sampling Bronx zip codes for positive virus test results, then building almost from the ground up Laplace’s quadratic approximation of our Bayesian likelihood estimation. In the process we check priors, write log likelihood functions, extract samples, predict outcomes, and watch a model completely fail its task by examining a predictive probability interval plot of a regression line. This will move us to build our interactive model into this Bayesian realm. Much to learn! We will continue to use the rethinking@slim R package from Richard McElreath to great advantage.
Video 2: Counting Uncertain Ways with Lagrange. In this episode we go over the basics of information uncertainty called entropy, find a useful measure of log likelihoods and compare some forecast models between two local rivals. Algebraic geometry raises its head here. No calculus, just arithmetic and a little algebra. Even log() is expressed as the simple polynomial \((5/2)(p - p^2) = H(p)\), our measure of information entropy.
Video 3: Watanabe’s Universal Inference Machine. Yes, the Widely Available Information criterion along with Leave-One-Out cross (entropy) validation and Pareto Smoothed Importance Sampling (Score) from Aki Vehtari et al. All on paper with pencil. Even Wilfredo Pareto shows up with the Genereralized Pareto Distribution to provide a principled way to deal with some bursts of logarithmic bits left on the table. Definitely check the arithmetic! Here are some notes: psis-waic.pdf
Video 4. Laffer and the implications of Taxable Inference. We finally get to R and some data. We stumble through Kullback-Leibler Divergence, offspring of Shannon Information Entropy, embedded in WAIC and PSIS. Some quap(), two or three models, including the use of Student’s t distribution to thicken a tail or two. Here is the R Markdown file for all of the code (it won’t compile very well without the images and cit.bib though): inference-above-and-beyond.Rmd
Video 5. Daniel Nettle on Language Diversity and Food. In this episode we walk through Week 4’s assignment. It is long, yes, but pulls together much of what we have building during the past few weeks. There are a lot of mechanics to getting to the overall assessment of which model best answers Nettle’s questions about language diversity and food. Language diversity is a measure of the diversity of cultures, here in each of 74 countries. Each language represents often centuries or more of a people’s world view applied to the concrete details of daily life as persons who participate in a community of persons. More that this language as culture will develop and be transmitted by the community over time. This data is a snapshot. We get to practice probabilistic inference, visualization of results, formation of hypotheses into statistical models, implementation of algorithms, and analytical stamina. Someone needs to build a system dynamics model of the relationships among language, food, land mass, and even terrain ruggedness. The Rmd and html files are in the assignment region of this Week 4 segment.
Reading is Fun
Counting on Laplace. We cover this reading in Video 1. Be sure you can run a
quap()model with the rethinking@slim R package!Inference Above and Beyond. A lot to cover here. We can get a glimpse of how difficult it is to compare two models by working through the Jill-Will forecast example. From there we get much more technical and land on Shannon’s information entropy. Definitely focus on the Laffer taxes and the Cassiopeia effect. A video will introduce the topics of information uncertainty, divergence, and deviance.
Let’s Do Somthing Interesting and Evaluate Our Progress
For those registered in a current Manhattan University MBA course, access the weekly grade assignment activity on the course Learning Management System (Moodle) and post your response there for credit. For those who are self-studying, you may access the Week 2 Workbook here.
Download the analysis of Nettle’s language diversity model: Rmd file and html rendering.
Statistically compare three models using WAIC, PSIS and building predictive probability intervals. We will use the Rmd file as a template. Be sure to upload load BOTH Rmd and rendered html files here:
Week 5
Reprieve and Revise!
This week we give ourselves a short reprieve. During this armistice we will
Review previous assignments and notes from Weeks 1 through 4
Note and attempt to fill gaps in our knowledge
Redo assignments as needed, including expanding on our examples, revising interpretations, and completing work partly finished
If any of us are on the R track then we will
Attempt to install the cmdstanr R package interface to the probabilistic programming library Stan. If not, we have not a few work arounds!
Begin to incorporate the R code from Acting on Bayes into our modeling of decisions and choosing models with WAIC (especially begin to think about highly volatile and improbable - uncertain observations in the 2 state decision model)
And if any of us are on the spreadsheet track then we will
Incorporate a simple grid approximation model into our spreadsheets
Measure information loss with WAIC and rebuild the volatility / uncertainty graph in a spreadsheet
Incorporate a 2-state / 2-decision model in out spreadsheets
Dates to Remember
Monday 2025-04-07 to Sunday 2025-04-13 online
Live session Saturday 2025-04-12 from 10:00 to 12:00 (Eastern Time; UTC -5) on Bill Foote’s Zoom link.
Zoom: https://us06web.zoom.us/j/4915046043?pwd=lRcmR6raK50vawabuxzl3fWECDGZYO.1
Enjoy the View
All videos are on the System Dynamics: Bayesian Inference and Calibration playlist on my Youtube channel. Here is the link to the playlist.
Video 1: Rethinking with Stan and friends. In this episode we trapse through the wickets of installing the Stan library and interfaces. We will be working with rstan, cmdstanr, and rethinking. Getting that C++ toolchain is the trick. Rtools43 on Windows is another. But it is all very well worth it!
Model for Video 2: Demo of J. Andrade tutorial.
Reading is Fun
Installation of CMDSTANR Package. Here is the Rmd file. With this file we will begin our journey to finally incorporating a full-blown nearly endogenous systems dynamics ODE model into our probabilistic inference engine.
Demo notes for J. Andrades **readsdr* tutorial. This is an extensive move into the inference workflow from xmile file to generative data on to actual 1918 H1N1 data all in Stan/cmdstanr.
Let’s Do Somthing Interesting and Evaluate Our Progress
This week’s assignment is finising assignments from Week 1 1 to Week 5. Have a nice week!
Weeks 6-7
BEING REMODELED AND REWRITTEN
Dates to Remember
Monday 2025-04-14 to Sunday 2024-04-27 online
Live session Saturday 2024-04-26 from 10:00 to 12:00 (Eastern Time; UTC -5) on Bill Foote’s Zoom link.
Zoom: https://us06web.zoom.us/j/4915046043?pwd=lRcmR6raK50vawabuxzl3fWECDGZYO.1
Enjoy the View
All videos are on the System Dynamics: Bayesian Inference and Calibration playlist on my Youtube channel. Here is the link to the playlist.
Video 1: Building up Hours, Forced Outages, and Restoration We finally get to the ultimate exercise: inference, and Bayesian at that. Here we plan our approach on paper with pencil. We started at the deep end of the pool with modeling dynamic, interactive, predator-prey behavior. We end this segment of our deliberations with an extension of this very same model as a compartment approach, but still it is predator-prey. We model reliability of technology using hours of operation as our norm. Forced outages take our operations partly off-line. We model the restoration process. Not surprisingly, the restoration is the logistic S-curve. Spread polynomials and Chebyshev polynomials (of the first kind) and chromogeometry anyone?
Video 2: Bringing the model to Vensim and R. We implement our paper and pencil model first in Vensim, then export the Vensim model to R using the readsdr package and its xmile file features. Some plotting using ggplot2 ensues. We peak at the observed data as well.
Video 3: How are things trending? From an article by John Sterman in 1986. - EXPECTATION FORMATION IN BEHAVIORAL SIMULATION MODELS, Sterman (1986) John Sterman develops the model as well in Business Dynamics, p. 634-643, with case studies following the baseline model. Here is an implementation of the model to highlight the character of initial conditions, and a switch to modify the initial present perceived present condition to change with changing inputs: Notes on behavioral expectation formation. The Vensim implementation is here: sterman-1986-expectation-formation-behavioral-simulation.mdl
Let’s Do Somthing Interesting and Evaluate Our Progress
The B Corp Project
Choose a B-Corp, NGO or not-for-profit organization. Formulate a question. Develop a quaestio disputata for the business question posed. This will be your frame for building a simulation. Be sure to at least use this outline from Foote’s beast or god paper (2024) where we might wander to pages 17-19 for some clarity around the frame of a quaestio disputata.
Using the many models here, and with the business canvas, produce a sector system, within which reside an inventory of sub-sector models. For example, the Key Partners sector (the Givers in our toy anthropology), might be modeled as a consortium which offers shared services; or the Actions / Resources sub-sectors might be modeled with available Work, finished work, rework and a resource for the project.
The Customers/Clients/(perhaps) Collaborators/Students/Patients (the Receivers) might be modeled as a cohort of adopters of an innovative technologically enabled product and/or service. We might note here that we don’t really communicate technologies from Givers to Receivers. We deal in actualities like products and services which are made available through a technology. The ordering (arrow directions) here is important when we apply overarching values (as in value propositions: say minimize the maximum grief of the most vulnerable) to the decisions we attempt to model.
You may use the evolving-b-corp.mdl model as a guiding template. Note that societal impact and value proposition views are left to you deft modeling capabilities.
You may use your own version of a Mooseco-WolfCo predator-prey model. For example, there seems to be some interest in modeling the dynamics of supply and demand with associated pricing to help compare buy, sell, hold decision alternatives. Here are two of these versions: supply-demand-price and MooseCo-WolfCo-limits
The Six-Step Model Development
- What is the business question in the form of a set of mutually exclusive decision alternatives? What are the four causes which define the approach to building your model? What are the key relationships among the terms involved in your approach (e.g., arrows connecting concepts)? What is an initial stock-flow-diagram of your approach? What graphs of look up tables and outcomes do you anticipate? Is this a system, and why (collection, connection, coherence)? Who is (are) making the decisions? How can they use the Bayesian decision analysis to inform their choice of potential decision alternatives?
Vensim >> R (or Spreadsheet) Model Implementation
- Build your implementation project model based on your 6-Step design. Outline and run three scenarios to assist with answering your posed business question. For each scenario discuss intended decision outcomes. How do the three scenarios together assist managers with answering the posed business question(s) and a prognosis for comparing decision alternatives. We might recall that the WAIC information approach cannot possibly select a decision – only a human is allow that privilege here. But the models and their predictive metrics can indeed inform a human decision maker (as opposed to some silicon-based consciousness on Alpha Centauri) with comparisons of the probably decision outcomes.
Management Recommendations
- Formulate three recommendations for management to answer the posed business question and associated decision alternatives.
Use the model scenario runs to support at least 3 pros and 3 con(tra)s regarding your response.
In your discussion of pros and cons, be sure to include appropriate traps we encountered in our reading and reflections on system archetypes. Be sure to order your recommendations according to importance (gravitas), requirements (auctoritas), and circumstances (adjunctes).
Finally, add recommendations for further work as well as at least three limitations to this analysis.
McElreath, Richard. 2020. Statistical Rethinking: A Bayesian Course with Examples in R and Stan. Second edition. CRC Press. https://xcelab.net/rm/statistical-rethinking/.
Copyright 2024, William G. Foote, all rights reserved.↩